

In the DECIMAL number system(Base 10), we easily picture the label 15 to count fifteen things like oranges or dollars.
We do the Base 10 calculation without too much stress on the brain.
15 = One times Ten PLUS Five times One = FIFTEEN.
We identify the column position, multiply the symbol there by the proper POWER of 10, and add things up to get the right quantity.
There are TEN UNIQUE SYMBOLS: 0,1,2,3,4,5,6,7,8,9 in the "Decimal Alphabet".
We have fingers one to ten, different from the symbols 0 to 9.
Zero causes confusion, because there is no "zero finger".
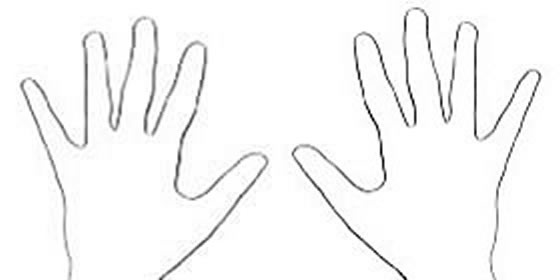
Ten in decimal(10) is a number that is represented by more than one symbol.
We start a new column to the left when we "run out" of unique symbols in the current column.
There is a ONES column, a TENS column, a HUNDREDS column, a THOUSANDS column, and so on.
Stick counting and Roman Numerals on the other hand are VERY challenging.
Stick counting is simple, but it is hard to write, read or tally very large quantities.
Roman Numerals, as seen on movie credits and college degrees, have complicated rules.
That causes stress for the brain, but we can figure out the "real" year if we are willing to translate.

Binary and Hexadecimal are like Decimal, with a slightly different "alphabet".
Binary has just two symbols. Hexadecimal has sixteen symbols.
There is a different BASE or Power for each column.
Calculation method is the same as decimal.
ON or OFF
YES or NO
TRUE or FALSE
"1" or "0"
They are like a Light Switch or several Light Switches.
Each Light switch is the same as a column.
Each column is a POWER of 2.
A switch can be ON or OFF.

With more switches, there are more possible combinations of ON and OFF.

Larger numbers can be represented by adding more switches.
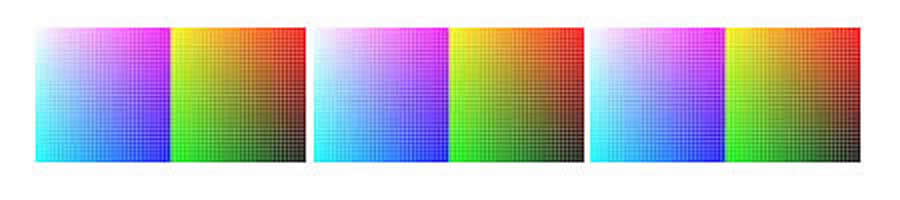
Things like colors can be represented by a number.
Computers have lots of switches.
So.....LOTS OF COLORS!
Counting method is same as for Decimal, except we have fewer symbols and more columns.
We identify the column position, multiply the symbol there by the proper POWER of 2, and add things up to get the right quantity.
Multiplying is easy because we only ever have to multiply by ONE.
ZERO is a placeholder, just like in Decimal.
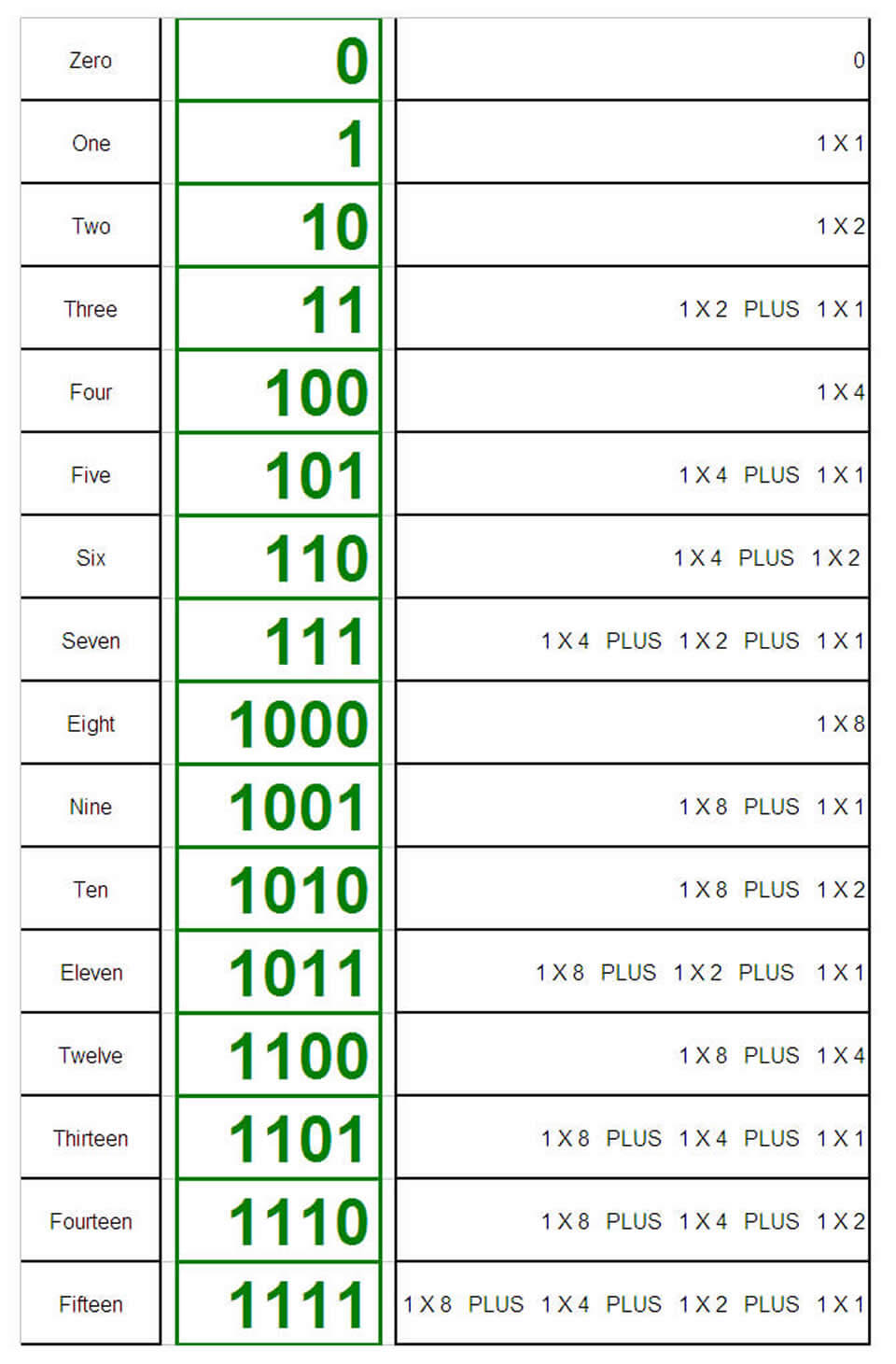
There is a ONES column, a TWOS column, a FOURS column, an EIGHTS column, a SIXTEENS column, and so on.
Just like in Decimal, we start a new column to the left when we "run out" of unique symbols in the current column.
Counting method is same as for Decimal, except we have MORE symbols.
We identify the column position, multiply the symbol there by the proper POWER of 16, and add things up to get the right quantity.
Calculating the quantity a Hexadecimal number represents is NOT intuitive or easy because we need six more unique symbols to represent the numbers ten through fifteen in each column.
Those symbols were arbitrarily chosen to be A, B, C, D, E and F, which do not look anything like symbols for numbers or quantities to just about everyone.
If we happened to have 8 fingers on each hand, this would make more sense for humans.
ZERO is a placeholder, just like in Decimal.
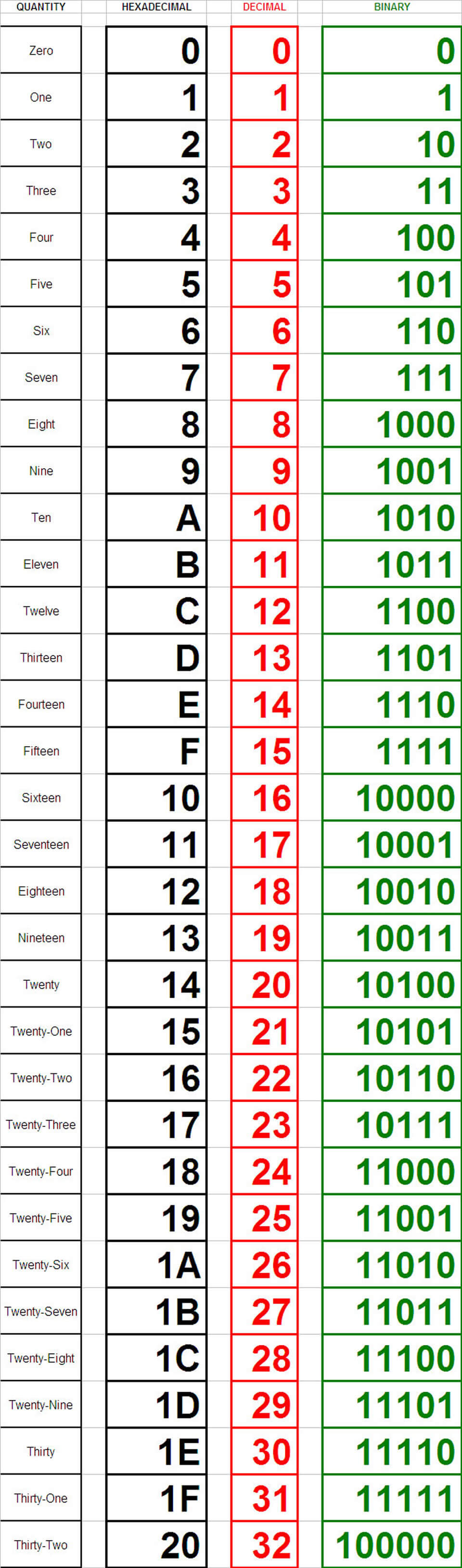
The first column(far right hand) is still the "ONES" column, or 16 to the zero power.
Next column to the left is the "SIXTEENS" column, or 16 to the first power.
Third column is the "256" column, or 16 to the second power.
Fourth column is the "4096" column, or 16 to the third power.
Fifth column is the "65536" column, or 16 to the fourth power.
The quantity 16 is 2 to the 4th power, 2 X 2 X 2 X 2, so one Hexadecimal symbol can be used to represent the same quantity as 4 Binary symbols.
From the table above, 20 in Hexadecimal = 100000 in Binary.
20 in Hexadecimal = (2 X 16) PLUS (0 X 1) = 32 in Decimal
Calculators can display and convert numbers from one number base to another. Just use the "Scientific View" to see how this works.
The binary representation can be split up every 4 digits, so 0010 0000 is 20 in Hex.
This happens to be useful for programmers and numbers people because a sequence of Hexadecimal symbols is easier to read than a string of Binary symbols.
You see Hexadecimal numbers in many places: Color charts, IP Addresses, MAC addresses, Identifiers and Computer code.
© 2009-2075 understandnumbers.com